zum Augustomagus-Bild hatte ich geschrieben:
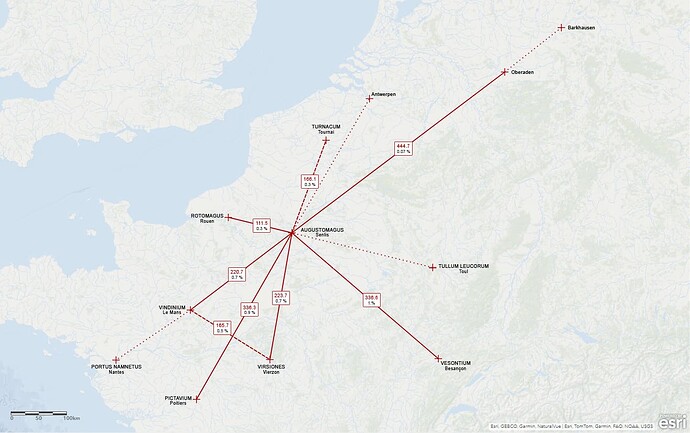
12 Punkte = 66 Entfernungen.
Davon 8 “interessant”.
Quotient = 0,12
Bei den Winkeln ist es schwierig erst mal die richtige Formel für die Gesamtzahl an Winkeln zu finden (damit man keine doppelt zählt).
Ich denke es müssten nx(n-2) Dreiecke [Probe: aus 3 Punkten entstehen 3x1 = 1 Dreiecke und aus 4 Punkten 4x2 = 8] und damit 3xnx(n-2) Winkel sein (Schnittpunkte ausgeklammert).
Für den Zähler des Quotienten würde ich (wenn man den Schnittpunkt Vindinium-Virsiones mit Augustomagus-Picatavium mitzählt) 4x90° und 5x180° zählen = 9.
Für den Nenner wäre das bei 13 Punkten: 429 Winkel.
Quotient = 0,03.
Ok, das ist falsch. Ich habe dabei anscheinend versucht die durch Dreiecke neu entstehenden Kreuzungspunkte und deren Unterdreiecke mitzuzählen.
Für eine einfache Betrachtung gilt dass jeder Eckpunkt mit zwei anderen Eckpunkten verbunden als Dreieck zählt. Das sind dann n x (n-1) x (n-2) und weil es egal ist mit welchem Punkt man anfängt und ein Dreieck dabei einmal linksherum und einmal rechtsherum gezählt wird gibt es n x (n-1) x (n-2) / 6 Dreiecke bei n Punkten. Probe: n=3 => 1, n=4 → 4 Dreiecke. Scheint plausibel.
Und jedes Dreieck hat 3 Winkel zu bieten. Also n x (n-1) x (n-2) /2
Wenn man das auf das Augustomagus-Bild anwendet: n=13 → 286 Dreiecke → 858 Winkel, in denen Du 9 “schöne” Winkel gefunden hast.
Quotient = 0,010489
Hoppla das ist π / 300 bei 0,1% Genauigkeit??? Bitte nachrechnen…
Aber Späßchen beiseite…
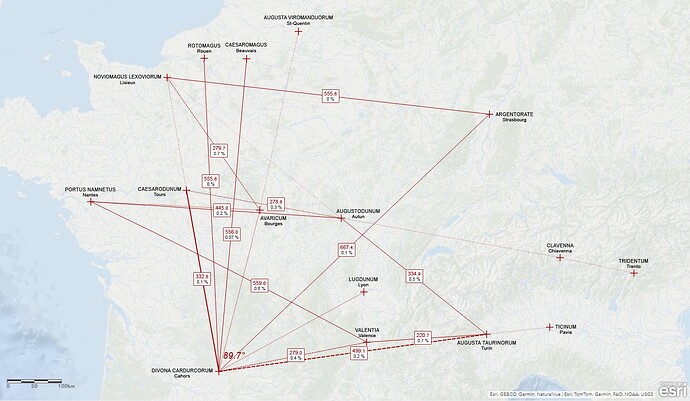
nach einem weiteren sehr erfolgreichen Arbeitstag hier das Ergebnis für den offensichtlich sehr relevanten Ort Cahors (Divona Carducorum [sic!]):
Jetzt gilt es auch hierzu den Quotienten der Entfernungen berechnen. Ich sehe 16 Punkte, wobei Du bei 4 davon gar nicht bei den Entfernungen berücksichtigt hast. Also nehme ich die mal raus. Bei n=12 gibt es 66 Entfernungen zu bestimmen. Davon hast Du 13 als “schön” ausgewählt. Das gibt einen Quotienten von 0,19
Das ist im Vergleich zu Augustomagus sogar höher und auch insgesamt erstaunlich hoch. Mein Bauchgefühl hätte deutlich weniger erwartet - aber sich darauf zu verlassen ist ja keine Wissenschaft…
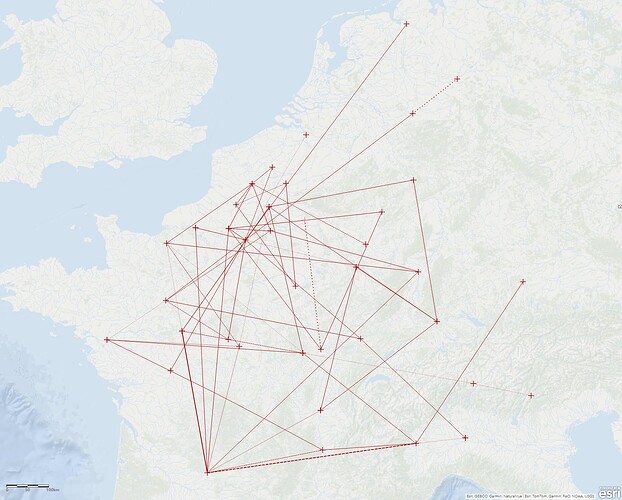
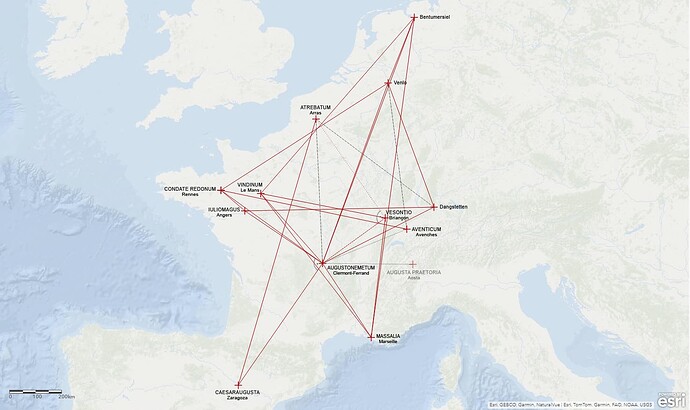
Aber was passiert wenn Du das Augustomagus und das Carducorum-Bild kombinierst? Soweit ich es überblicke gibt es keine gemeinsamen Punkte so dass also in Summe 12+12=24 Punkte sind. Damit gäbe es 276 Entfernungen. Davon sind 8+13 = 21 “schön”. Aber das sind ja sicher nicht alle weil Du das nach einander und unabhängig erarbeitet hast.
Vielleicht kannst Du im letzten Bild einfach mal zählen wieviele Deiner Entfernungen Dein Kriterium erfüllen und wieviele Punkte dabei berücksichtigt sind.
Da bin ich gespannt wie dann der Quotient aussieht.
Je länger ich mir Senlis anschaue, desto mehr kommt da zu Tage.
