@ Geognost
Diese offizielle Version hat schon Theodor Mommsen angezweifelt:
Was Mommsen schreibt ist doch genau die offizielle Version !! ???
Als die Römer dort ihre Lager, Strassen und Brücken bauten verwendeten sie die Meile. 
Oder haben dort “gallische” Billiglöhner mit der Leuge vermessen?
Wenn das Caesar gewußt hätte ! >:)
Idealerweise hätte den 53.13°-Winkel auf der Schiineflue ermittelt und dann die Basislinie von dort vermessen. Der dritte Punkt w . ar dann erreicht, wenn die Jungfrau genau querab lag, nämlich in Rüti bei Büren. Hier könnte eine Menge Trial-and-error im Spiel gewesen sein, und es Glück twa.
Das ist gehoppt wie gesprungen. Man muß so oder so in Richtung zum anderen Messpunkt peilen und die Luftlinie ermitteln. Ich bezweifle sehr, dass man auf 60 km noch ein Feuer oder einen Turm anpeilen kann ohne Fernglas.
Aber selbst wenn war da noch der arme Reiter, der zum “Johannisfeuer” ritt und sagen mußte, dass das Feuer ausgemacht werden soll und weiter nach rechts muß. Bei einem Turm hätte man das Trumm dann schon fahrbar machen müssen. Und die armen Pferde erst ! Da bringst du alle Tierschutzmuttis gegen dich auf ! 
Die Entfernungen von 60 bis 130 km stören mich überhaupt an dieser ganzen Vermesserei.
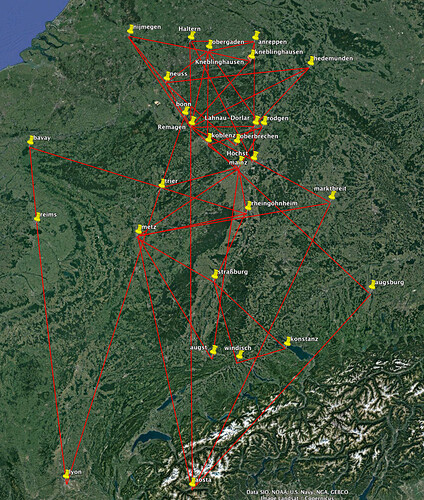
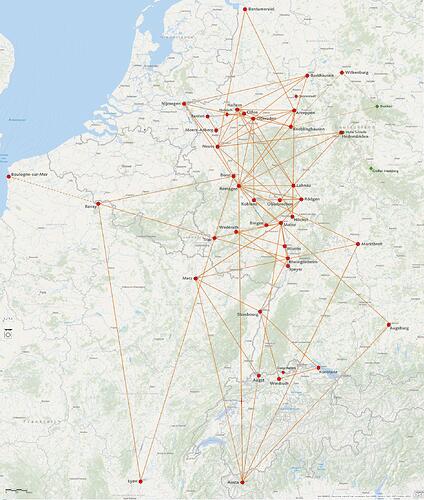
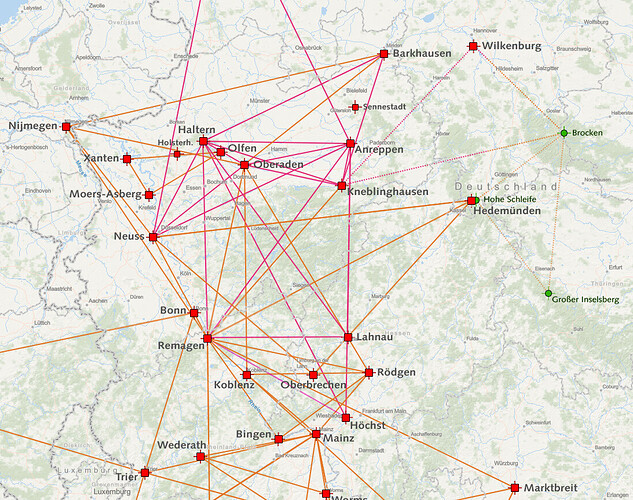
Nehmen wie Haltern, Barkhausen und Kneblinghausen. Dort müßte man Sichtweiten von ca.90 bis ca. 130 km haben. Glaubst du wirklich, dass man da ein Lager mit seinen Türmen noch mit bloßem Auge ausmachen kann. Wenn nicht, dann hatte man keine blasse Ahnung wohin man peilen muß, geschweige denn, dass ich einen Winkel festlegen kann. Ich halte diese Dreiecke nach wie vor einen Zufall.
Bestärkt hat mich darin das Dreieck Marktbreit nach Welzheim usw… wie auch Marktbreit ins Rheintal.
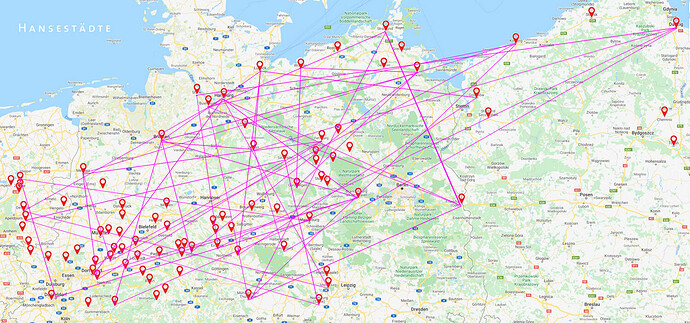
Jetzt mal zu Angelas Vernetzung der Lager. Hier komme ich noch mal zurück auf meine “Phantasiekarte” der vielen Marschlager.
Wenn die Römer überhaupt die Triangulation zur Raumvermessung eingesetzt haben, dann nur von kleinen Dreiecken aus, die sie über die Marschlager ermittelten. Das setzt aber voraus, dass man dort Türme baute, die über die Baumkronen ragten. ( Vermessung Indiens ! )
Deine schönen Weidewälder halfen da nichts, denn ich hatte ja keine Ahnung in welcher Richtung ich durch den Wald peilen mußte. Ich glaube von der Idee, dass die Römer beim Vormarsch quer durch Wald und über Berge vermessen haben sind wir abgekommen, oder !!?? 
Auf diese Weise konnte ich die Lager anpeilen, Winkel ermitteln. Mit dem Winkel mußte ich jetzt ein Laber am Boden anpeilen und die Gerade abmessen. Dann konnte ich mit dem Abitur der höheren Hilfsschule die Seiten des Dreicks berechnen. ( Kanns de auch mit de Google machen !  )
)
Eingenordet erstelle ich auf diese Weise ein Netz aus kleinen Dreiecken, in die dann auch deine eingebettet sind.
Trianulation
https://dewiki.de/Lexikon/Triangulation_(Geodäsie)
ZITAT:
Theodolit die Winkel zwischen sämtlichen hier endenden Dreiecksseiten ermittelt, indem die jeweils anderen Punkte der Seite angezielt werden. Dazu müssen die Punkte untereinander freie Sicht haben…
der Regel wird das Dreiecksnetz überbestimmt, das heißt, es werden nicht nur die Dreiecke bestimmt, die…In __ zu einer einfachen Überdeckung des Messgebietes notwendig sind, sondern alle, die sich durch die gegenseitige Beobachtbarkeit der Punkte ergeben. So kann durch Ausgleichsrechnung die Genauigkeit gesteigert werden…
_…Das so bestimmte Dreiecksnetz ist das Netz 1. Ordnung. Da seine Punkte sehr weit voneinander entfernt liegen, wird es wiederum durch Triangulation verdichtet zu einem Netz 2. Ordnung mit einem Punktabstand in der Größenordnung von 10 Kilometer, und dieses wiederum zu weiteren Netzen mit geländeabhängigen Punktabständen. _ ENDE
Ich glaube aber nicht an die Großvermessung und gehe deshalb von Zufällen aus. Siehe oben Marktbreit. Andererseits setzt du Bergvermessungen voraus, die aber viel zu lange Strecken zu einem sichtbaren Punkt zum anderen ergeben.
Last batten und liest, es ist nichts, aber auch gar nichts an Quellen bekannt, die eine solche Vermessung auch nur ansatzweise schildern. Selbst Velleius Paterculus, Reiterpräfekt der als Legatus acht Jahre lang in Germanien diente ( bis 9 n. Chr.) berichtet nichts davon.
Ich habe fertig ! Schnapsflasche leer ! 
Gruß
Kurti
Nachtrag:
Auch deine Städte in Gallien wurden nicht gleichzeitig gebaut, denn du mußt den keltischen Bestand mitzählen. Die Dreiecksbeziehung bestand also schon !
Ansonsten mußte man querfeldein und über Berge immer in gerader Linie den neuen, römischen Lagerbau bis nach Metz oder wohin auch immer vermessen, um das sichtbar zu machen.
Außerdem ist es bei der Ausdehnung der heutigen Städte nicht leicht den Mittelpunkt festzulegen. Bei den Vermessungen der Herzogtümer war es meistens die Kirche oder die größte Kathedrale. Gesehen werden war wichtig ! 




 )
)
